Should I Buy or Should I Rent?

One simple way to look at it is to purely consider the costs, ignoring real estate price developments and opportunity costs.

The biggest costs related to buying are interest payments and transaction costs that incur when buying (and potentially selling). Additionally, there are maintenance costs and other costs such as insurance that a renter doesn't pay. At least not directly. If you rent, you pay the rent and that's it. Variable costs like heating, house management and so on are the same in both cases, so they are not considered. The table below shows the results for combinations of time and prices. The transaction cost would occur again if you at some point sell. However, I have not included this since the option is always there to instead rent out.

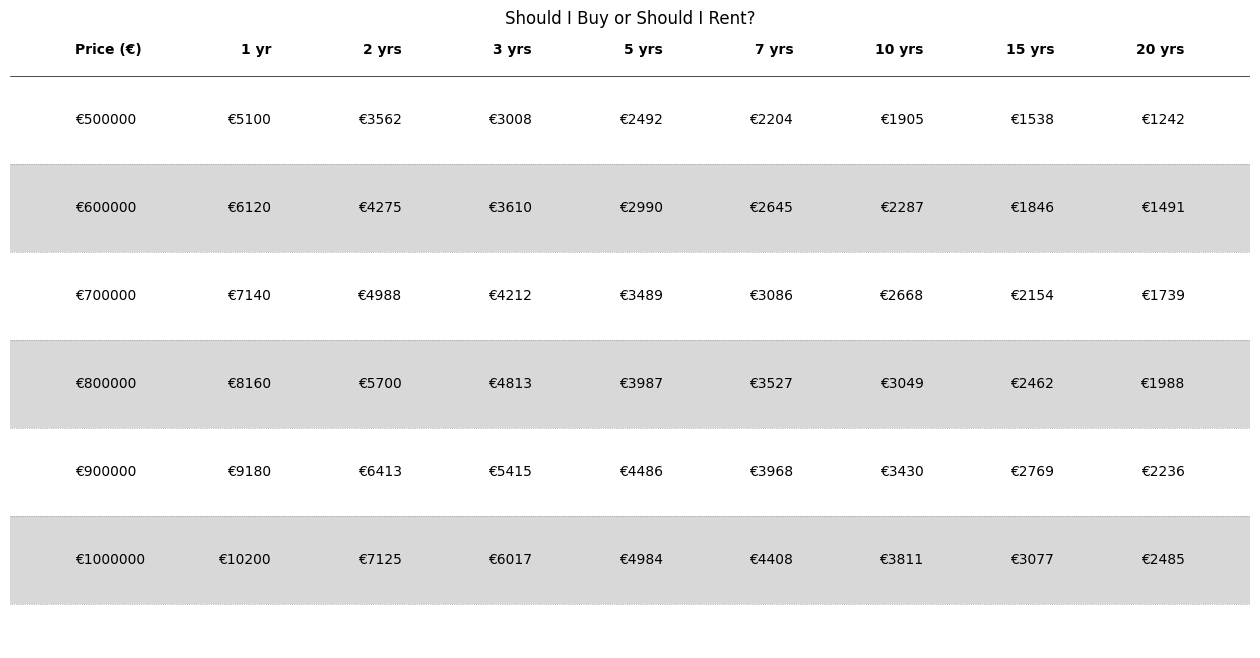Let's take a look at one cell and break down the calculation and the sources of the numbers. With an expected time horizon of 7 years in a flat worth €800'000. The table shows €2'871. This number is what I should be willing to pay in rent, assuming yearly 2% rent increases, for an equivalent flat instead of buying. Any more than that, I would rather buy.

In scenario for all these calculations I assume the following:

• A 7% transaction cost rate, which covers notarius, taxes and real estate agent fees. An arbitrary calculator from a German bank operates with roughly 8.5% so 7% is a fairly low estimate.
• The mortgage rate I use is 3.6% over 20 years. Again, based on an online calculator for a mortgage.
• Additionally, I added 0.5% for yearly maintenance and other ownership costs such as insurance.

Together, this gives a yearly cost of 4.1% of the value the purchase price per year and a one-time cost of 7% of the price as transaction costs. I then have the total cost of owning and buying for the given time horizon, 7 years in this case. To get the equivalent rent I should be willing to pay now, I assume a 2% yearly rent increase and solve the simple equation:

\[ \sum_{i=1}^T \text{yearly rent} * 1.02^i = \text{total cost}\]

In other words, what should I be willing to pay in rent now assuming a 2% yearly increase for a flat that I could buy for €800'000 where I plan to live for 7 years? Not more than €2'871.

The simple analysis has a big flaw in that it doesn't consider housing price growth. A common argument for buying is that real estate prices tend to increase over time and that you are more or less guaranteed to get your money back. The simple analysis can therefore easily be brushed aside. To avoid that, let's add the potential capital gains (or losses) to the mix. Crucially, let's do it with a reasonable alternative scenario meaning not assuming that the money otherwise would be spent or sit in the bank, which seems to be the common benchmark. Let's consider the following two scenarios and see how it impacts your wealth:

1. Buying a property starting with 85% mortgage paid down over 20 years.
2. Investing the money that would otherwise go towards mortgage payments in a global ETF and the difference between purchasing and renting costs.

We do the same analysis as above, but we now include the opportunity cost (or benefit) as another cost of buying and owning a property. We look at a flat that costs €800'000¹. The opportunity cost is just the returns from scenario 2, investing in the market, minus the returns from scenario 1, buying a property. This can of course be a negative cost, which means that housing was the better investment. The graph below shows different scenarios. Each line shows how the opportunity cost changes over time. For example, take the line labeled 2003. What is shown here is how the opportunity cost would develop over time, if you bought a house (or started renting and instead invested in the DAX) in 2003 until today. In this particular case, the opportunity cost is almost €1'000'000, but this is the most extreme case.

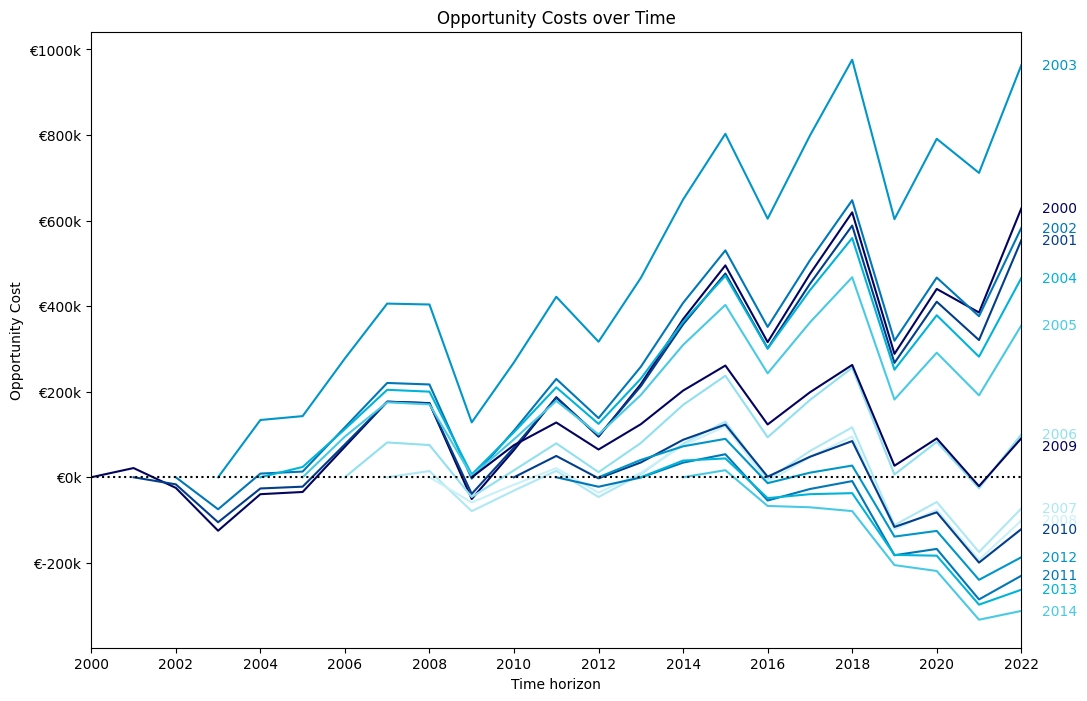Another interesting reading from the chart is how the opportunity cost develops over time. The outcomes are almost sorted by the starting year. In other words, in recent years buying was preferable compared to investing in the market and renting. However, the S&P500 was up 250% while the OBX (Oslo Børs) is up almost 400% instead of the DAX's 150% return.

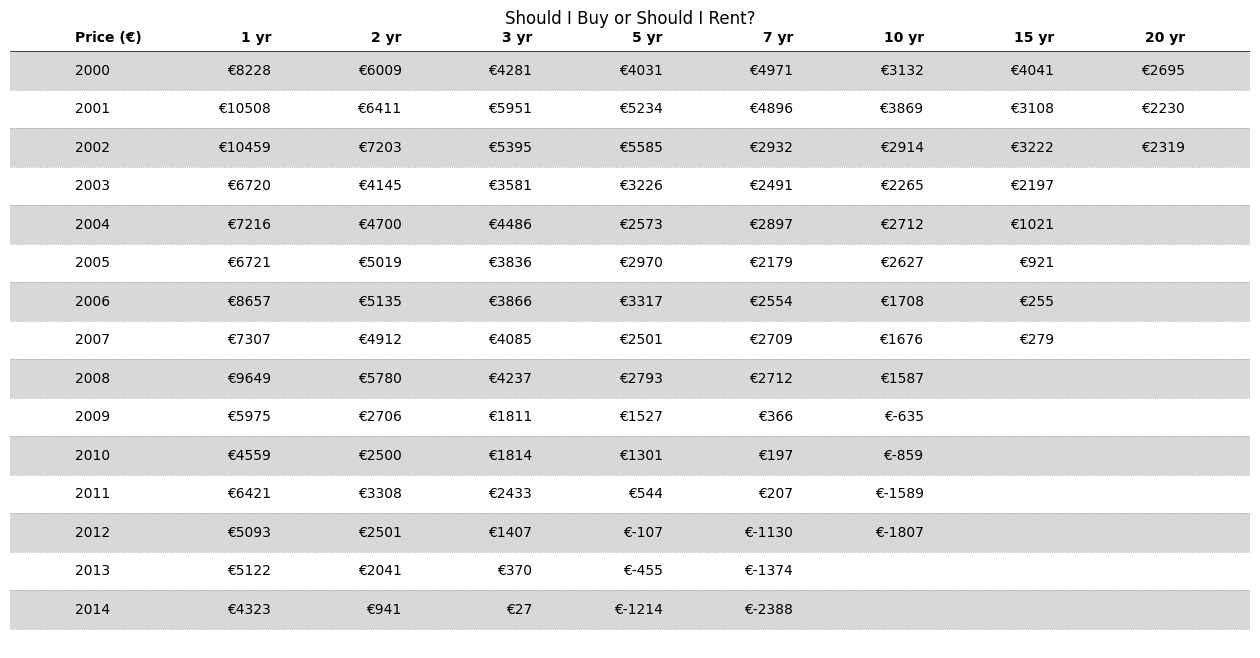The decision table changes drastically. The rows are now the scenario while the price is still fixed at €800'000. We now see that for recent years the equivalent rent is negative, meaning that even if someone paid you to live in their apartment you should still prefer to buy! In other words, the scenarios make all the difference and if you bought 10 years ago that might have been a life-changing decision (although Bitcoin would have been even better).

In the end, it all comes down to the time horizon. The longer the time horizon the more time you have to spread out transaction costs and it is less likely is that your house will lose value. Conversely, if you are renting with a long-term horizon the longer your rent have increased. To be succinct, the rent only increases while the purchasing costs go down over time. However, if you consider the opportunity cost it is still not obvious what the better choice is. The last 20 years showed that in recent years buying was the better option so if we see similar developments going forward go buy a house! On the other hand, if we see similar developments as in the noughties, investing in the market is the better option by far.

In the end, it is an emotional decsion. What is the value of having your own place? And on the flip side, what is the value of the flexibility of renting a place and easily moving? This allows upsizing and downsizing more easily. In the simple analysis, if I can afford to buy for €800'000 I should be willing to pay rent up to €2700 with a time horizon of 8 years, but for that rent I can rent a place that is worth quite a bit more than €800'000!

So if you found a property that you could imagine staying in forever and you can afford to buy it, it is probably a good idea. There are other benefits to owning your own home. It is a real asset that in the end is completely yours and you can treat it accordingly. No need to ask the landlord if you want to renovate or rent it out for a couple of years. It is up to you. Renting on the other hand gives flexibility and potentially less stress (at least in a country like Germany where renters are well-protected)